Difference between revisions of "Sigma 6"
From wikikotten
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | |||
| + | [http://en.wikipedia.org/wiki/Standard_deviation Standard deviation] | ||
| + | |||
===Rules for normally distributed data=== | ===Rules for normally distributed data=== | ||
| − | [[Image:standard_deviation_diagram. | + | [[Image:standard_deviation_diagram.png|thumb|350px|Dark blue is less than one standard deviation from the mean. For the [[normal distribution]], this accounts for 68.27% of the set; while two standard deviations from the mean (medium and dark blue) account for 95.45%; and three standard deviations (light, medium, and dark blue) account for 99.73%.]] |
In practice, one often assumes that the data are from an approximately [[normal distribution|normally distributed]] population. If that assumption is justified, then about 68% of the values are within 1 standard deviation of the mean, about 95% of the values are within two standard deviations and about 99.7% lie within 3 standard deviations. This is known as the '''"68-95-99.7 rule"''', or '''"the empirical rule"''' | In practice, one often assumes that the data are from an approximately [[normal distribution|normally distributed]] population. If that assumption is justified, then about 68% of the values are within 1 standard deviation of the mean, about 95% of the values are within two standard deviations and about 99.7% lie within 3 standard deviations. This is known as the '''"68-95-99.7 rule"''', or '''"the empirical rule"''' | ||
Latest revision as of 01:52, 2 April 2007
Rules for normally distributed data
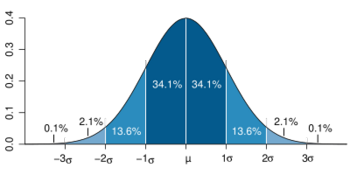
Dark blue is less than one standard deviation from the mean. For the normal distribution, this accounts for 68.27% of the set; while two standard deviations from the mean (medium and dark blue) account for 95.45%; and three standard deviations (light, medium, and dark blue) account for 99.73%.
In practice, one often assumes that the data are from an approximately normally distributed population. If that assumption is justified, then about 68% of the values are within 1 standard deviation of the mean, about 95% of the values are within two standard deviations and about 99.7% lie within 3 standard deviations. This is known as the "68-95-99.7 rule", or "the empirical rule"
The confidence intervals are as follows:
| σ | 68.26894921371% |
| 2σ | 95.44997361036% |
| 3σ | 99.73002039367% |
| 4σ | 99.99366575163% |
| 5σ | 99.99994266969% |
| 6σ | 99.99999980268% |
| 7σ | 99.99999999974% |
For normal distributions, the two points of the curve which are one standard deviation from the mean are also the inflection points.